Weighing the Earth

Shortly after the time of the American Revolution, an ambitious idea began to form in the mind of Henry Cavendish.

"I am trying to find the density of the Earth," he rather humbly stated. As bold as that goal might seem, it actually wildly undersells what Cavendish ended up doing. This would be a bit like how Pierre-Simon Laplace had recently estimated the average depth of the oceans on the planet.

His idea was that the gravitational pull of the Moon and Sun influenced the Earth’s oceans, inducing them to slosh around at regular intervals.

By thinking carefully and deeply, Laplace reasoned that the speed of tidal waves depended on how deep the water was, and he knew that he could simply invert his equation to figure out the ocean’s average depth.

His equations told him that the average depth was around 4 KM, and it turns out to be about 3.7 KM.

Cavendish would have heard about Laplace’s incredible mental feat—not just because it was a truly incredible example of what you could determine with limited information, but also because Laplace was something of a social butterfly. He ran in the right circles to be widely published and read.

Cavendish, by contrast, was so much of a hermit that he passed notes to his female staff instead of speaking, and this was the primary way he communicated with the outside world. All this reclusion gave him a lot of time to think, and it must have shaped the very way he thought.

For this reason, much of Cavendish’s brilliance was unknown during his lifetime. James Clerk Maxwell read through his old notebooks and realized that Cavendish had independently developed a significant portion of modern physics, including deriving Ohm’s Law and Coulomb’s Law.

He was a bit like the Van Gogh of physics.

So, when he said he was going to find the density of the Earth, it’s perhaps understandable that Cavendish might undersell the importance of what he was truly doing.

In fact, it might be more accurate to say that Cavendish was going to weigh the Earth. That’s because he would need to know the mass of the Earth before being able to calculate its average density, just as Laplace had needed to know the circumference of the Earth before he could calculate the relative speed of the tidal waves.

Leave it to Cavendish—the guy who had invented techniques and derived equations that are now central to modern physics, but had neglected to tell the world about them—to miss such a branding opportunity. Weighing the entire planet (which we happen to be on) certainly sounds more impressive than finding the average density.

Even weighing the Earth dramatically undersells the importance of what Cavendish truly found.

When Newton derived his equations for gravity, he described how two objects will be attracted to one another by a force that’s inversely proportionate to the square of the distance.

This tells you a lot about the way gravity works, but it doesn't say anything about how strong the force itself is. Sure, it goes down as you move objects away from one another, but how strong is that force to begin with? To figure that out, you needed to have G, the gravitational constant.

“Weighing the Earth” was quaint, but what Cavendish accomplished by calculating this important constant for the first time is so much more impressive.

You’ve been patient for long enough, so let’s talk about how he did this.

As circumstances would so often have it, the apparatus Cavendish would need had just recently been invented by Sir John Michell. Michell had developed a friendship with Cavendish, and the two would discuss wild ideas at the forefront of scientific thought. One of these wild ideas was the concept of a black hole.

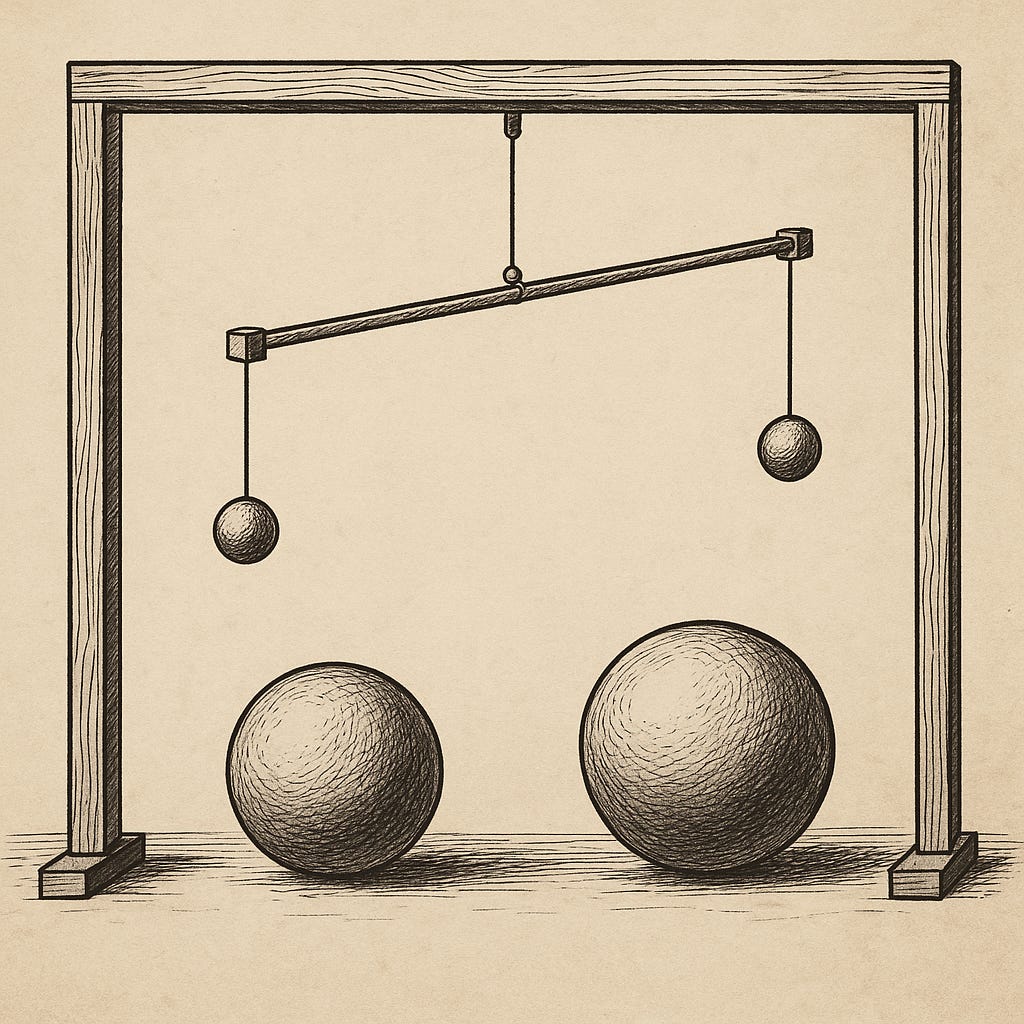
Anyway, Michell badly wanted to understand how powerful G was. He came up with a clever device called a torsion balance, which was a horizontal rod suspended from a thin wire, and with tiny lead balls on either end. Michell died before he could complete his experiment to measure this fundamental force, but Cavendish was the perfect hermit for the job.

Cavendish either inherited Michell’s device, or he had a similar one made. Either way, he placed larger lead spheres nearby, causing the bar to twist just the tiniest bit. Since he knew the masses of the balls and the distances between them, it was now a simple matter of math to calculate how much G pulled on those balls.

Now, Cavendish had this measurement! Now, he could use this to calculate the weight (and density) of the Earth.